Techniki dyfrakcyjne pozwalają obrazować sieć odwrotną kryształu. Dla sieci krystalicznej rozpiętej przez wektor translacji:
\[\mathbf T=u_1 \mathbf{a} + u_2 \mathbf{b} + u_3 \mathbf{c}\]
gdzie a, b, c są wektorami prostymi sieci, u1, u2, u3 są liczbami całkowitymi, wektory podstawowe sieci odwrotnej dane są zależnościami:
\[ \mathbf a^*= \frac{2 \pi}{V}\mathbf b \times \mathbf c \]
\[\mathbf b^*= \frac{2 \pi}{V}\mathbf c \times \mathbf a\]
\[\mathbf c^*= \frac{2 \pi}{V} \mathbf a \times \mathbf b\]
gdzie:
\[V=\mathbf a \cdot(\mathbf b \times \mathbf c)\]
Dla powierzchni kryształu, która tworzy sieć dwuwymiarową, wektor c dąży do nieskończoności. Wektor c* będzie wówczas dążyć do zera, co sprawia, że sieć odwrotna do sieci płaskiej ma postać układu prostych zwanych prętami, rozłożonych w przestrzeni w periodyczny sposób. Wektory sieci odwrotnej w takim przypadku przyjmą postać:
\[\mathbf a^*= \frac{2 \pi}{S}\mathbf b \times \mathbf n\]
\[\mathbf b^*= \frac{2 \pi}{S}\mathbf n \times \mathbf a\]
\[\mathbf c^* \rightarrow 0\]
gdzie:
\[S=\mathbf a \cdot(\mathbf b \times \mathbf n)\]
jest polem powierzchniowej komórki elementarnej, n jest wektorem jednostkowym prostopadłym do powierzchni.
Warunek Bragg'a przy odbiciu od sieci krystalicznej ma postać [1]:
\[\mathbf{\Delta k}=\mathbf{G}\]
gdzie wektor \[ \mathbf{G} = u_1 \mathbf a^* + u_2 \mathbf b^* \] jest analogiem wektora translacji T dla sieci odwrotnej. \[ \mathbf{\Delta k}= \mathbf{k}_f-\mathbf{k}_0 \], przy czym wektory \[ \mathbf{k}_0 \] oraz \[ \mathbf{k}_f \] oznaczają wektor falowy promieniowania padającego oraz odbitego od kryształu. Spełnienie warunku Bragga jest warunkiem koniecznym powstania wierzchołka interferencyjnego.
Geometryczna interpretacja warunku Bragga zwana jest konstrukcją Ewalda. Pozwala ona wyznaczyć kierunki, w których następuje konstruktywna interferencja fal elektronowych. Rysunek 1 przedstawia sferę Ewalda o promieniu \[ |\mathbf{k}_0| \], która jest ,,zanurzana'' w sieci odwrotnej w postaci periodycznie rozłożonych prętów. Punkty przecięcia sfery z prętami zrzutowane na ekran tworzą układ plamek dyfrakcyjnych.
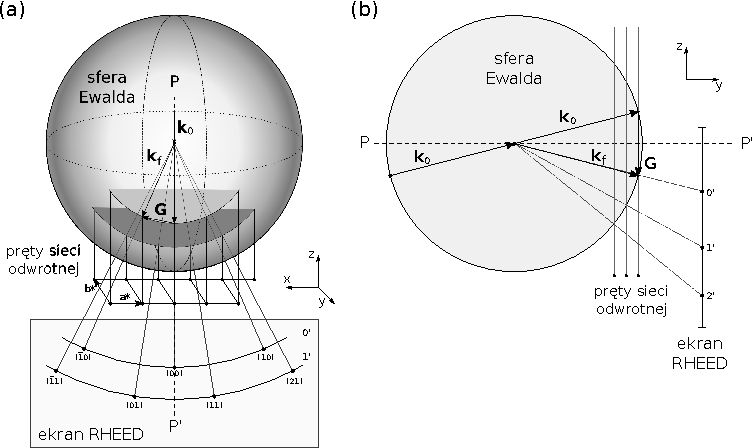
W warunkach prowadzonych eksperymentów elektrony przyspieszane są napięciem U=18 kV, zatem pojedynczy elektron posiada energię kinetyczną równą E=18 keV. Energia kinetyczna elektronu dana jest przez zależność:
\[E_{kin}=\frac{\hbar^2 |\mathbf{k}_0|^2}{2m}\]
gdzie \[ \hbar \] to stała Plancka podzielona przez \[ 2 \pi \], \[ |\mathbf{k}_0| \] to wartość wektora falowego, m jest masą elektronu. Przekształcając powyższą zależność można wyznaczyć wartość wektora falowego elektronu:
\[|\mathbf{k_0}|=\frac{\sqrt{2mE_{kin}}}{\hbar}\]
Promień sfery Ewalda ma zatem wartość: \[ |\mathbf{k}_0| = 68,7 \] A-1.
Wyznaczenie składowych x oraz z położenia maksimów interferencyjnych na ekranie RHEED pozwala na wyznaczenie składowych x, y, z wektora \[ \mathbf{\Delta k} \]. Do tego celu należy posłużyć się poniższymi zależnościami:
\[\Delta k_x=k_0 (\sin \varphi_f)\]
\[\Delta k_y=k_0 (\cos \varphi_f \cdot \cos \theta_f - \cos \theta_0)\]
\[\Delta k_z=k_0 (\cos \varphi_f \cdot \sin \theta_f - \sin \theta_0)\]
gdzie \[ k_0=|\mathbf{k}_0| \] jest wartością wektora falowego dla elektronów kierowanych na próbkę (zakłada się jedynie odbicia elastyczne), \[ \theta_0 \] jest kątem padania, znaczenie kątów \[ \theta_f \] oraz \[ \varphi_f \] zostało zilustrowane na rysunku 2. Kąty te mogą zostać obliczone na podstawie położenia punktów na ekranie przy wykorzystaniu zależności:
\[\tan \theta_f= \frac{z_f}{L}\]
\[\tan \varphi_f= \frac{x_f}{L}\]
W opisywanej aparaturze odległość próbki od ekranu wynosi: L= 38,5 cm.
 Rys. 2. Zależności geometryczne między położeniem plamek dyfrakcyjnych a kątami.
Rys. 2. Zależności geometryczne między położeniem plamek dyfrakcyjnych a kątami.
Przedstawione wyżej rozważania pozwalają na obliczenie wartości zmiany składowych wektora falowego dla elektronów tworzących kolejne punkty na ekranie. Zgodnie z warunkiem Bragga różnice między kolejnymi wektorami \[ \mathbf{k}_f - \mathbf{k}_0 \] muszą być równe wektorowi translacji sieci odwrotnej \[ \mathbf{G} \]. Stąd możliwe jest wyznaczenie wektorów podstawowych \[ \mathbf a^* \] oraz \[ \mathbf b^* \] powierzchniowej sieci odwrotnej i w kolejnym kroku wektorów podstawowych sieci rzeczywistej.
Powyższa interpretacja zakłada wyidealizowane warunki eksperymentalne: występowanie tylko elastycznych rozproszeń elektronów, brak rozrzutu energetycznego elektronów w wiązce, nieskończone wymiary powierzchni kryształu oraz idealne uporządkowanie powierzchni. W rzeczywistym przypadku część elektronów jest rozpraszana nieelastycznie, istnieje też oddziaływanie wiązki z fononami, energie elektronów podlegają również pewnemu rozrzutowi temperaturowemu. Efekty te sprawiają, że obrazy RHEED zawierają zawsze pewien poziom tła, widoczne są na nim również linie związane z nieelastycznym rozpraszaniem. Obserwowane wierzchołki dyfrakcyjne mają zwykle postać elips, bądź krótkich odcinków. Pozwala to na uzyskanie informacji między innymi na temat stopnia uporządkowania powierzchni kryształu.
[1] C. Kittel, IWstęp do fizyki ciała stałego, (Wydawnictwo Naukowe PWN, Warszawa, 1999)


