Położenie atomów w komórce elementarnej, płaszczyzny w krysztale, a także kierunki krystalograficzne, określa się przy pomocy wskaźników Millera.
Jeśli chcemy określić rodzaj płaszczyzny w pierwszej kolejności odnajdujemy jej punkty przecięcia z osiami poprowadzonymi wzdłuż wektorów \( \vec{a} \), \( \vec{b} \), \( \vec{c} \), wyskalowanymi w stałych sieci. Następnie odwrotności otrzymanych liczb sprowadzamy do najmniejszych liczb całkowitych o wspólnym mianowniku, a liczniki otrzymanych liczb zapisujemy w okrągłych nawiasach. Poniżej zamieszczono przykład ilustrujący poszczególne kroki.
Rysunek 1 przedstawia płaszczyznę przecinającą osie a, b, c w punktach: 3, 3, 5. Zapisujemy odwrotności tych liczb: 1/3, 1/3, 1/5. Sprowadzamy liczby do wspólnego mianownika o minimalnej wartości 5/15, 5/15, 3/15. Liczby stanowiące liczniki poszczególnych ułamków zapisujemy w okrągłych nawiasach i stanowią one poszukiwane wskaźniki Millera dla wybranej płaszczyzny (553).
W podobny sposób w kryształach określane są kierunki, przy czym liczby zapisywane są wówczas w nawiasach kwadratowych (np. [111]).
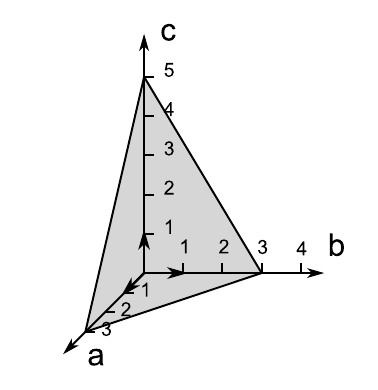 Rys. 1. Płaszczyzna (553)
Rys. 1. Płaszczyzna (553)
Struktura HCP
Kierunki krystalograficzne oraz oznaczenie płaszczyzn w strukturze heksagonalnej gęstego upakowania (HCP) wygodnie jest przedstawić w tzw. notacji czterowskaźnikowej zwanej również wskaźnikami Millera-Bravais'go. Wykorzystanie tej notacji ułatwia ocenę, które płaszczyzny lub kierunki należą do tej samej rodziny (są równoznaczne w strukturze HCP).
Oznaczenie płaszczyzn krystalograficznych
Na rysunku 1 zaznaczono w komórce elementarnej HCP podstawowe wektory translacji \(\vec a_1\), \(\vec a_2 \) oraz \(\vec c\). Wektory \(\vec a_1\) oraz \(\vec a_2 \) leżą na tej samej płaszczyźnie natomiast kąt między nimi wynosi \(120^{\circ}\). Dla ustalenia uwagi w komórce elementarnej zaznaczono płaszczyzny o wskaźnikach Millera \((001)\) oraz \((1 \bar 1 0)\). W celu lepszej przejrzystości te, oraz inne ściany zostały podpisane na środkowym schemacie, który przedstawia widok z góry na komórkę HCP. Można łatwo zauważyć, że mimo, że wszystkie ściany charakteryzują się tą samą symetrią to ich wskaźniki (H oraz K) są złożone z permutacji liczb \(1, 0\) lub \(-1, 1\). Z tego powodu trudno dostrzec ich podobieństwo.
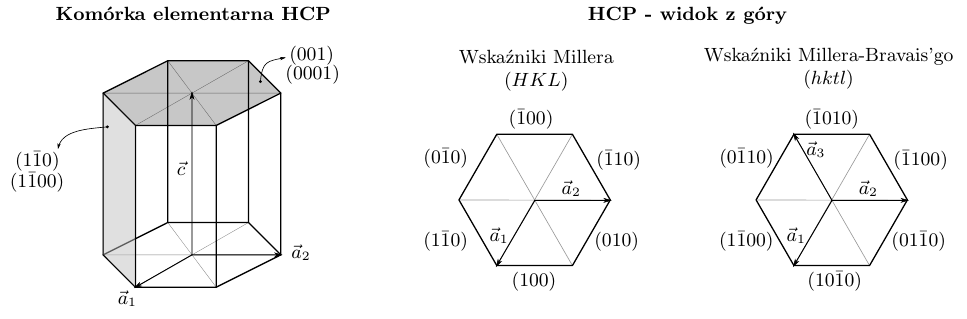 Rys. 1. Oznaczenie płaszczyzn w notacji Millera oraz Millera-Bravais'go dla struktury HCP.
Rys. 1. Oznaczenie płaszczyzn w notacji Millera oraz Millera-Bravais'go dla struktury HCP.
Dla podkreślenia symetrii struktury można wprowadzić dodatkowy wektor translacji \(\vec a_3 = - (\vec a_1 + \vec a_2)\). Wówczas pojawi się dodatkowy wskaźnik \(t\), którego wartość wyznaczymy z relacji \(t= - (H + K)\).
Zastosowanie notacji czterowskaźnikowej ułatwia dostrzeżenie podobieństwa między poszczególnymi płaszczyznami. Widzimy, że w powyższym przypadku (prawy schemat na rys. 1) wszystkie ściany są opisane przez permutację liczb: \(1, -1, 0\) (mowa jest o pierwszych trzech liczbach: \(h\), \(k\), \(t\)).
Przejście z notacji trójwskaźnikowej \((HKL)\) do notacji czterowskaźnikowej \((hktl)\) można wykonać przy pomocy poniższych wzorów:
\(h = H \) , \(k = K\) , \(t = - (H+K)\) , \(l = L\)
Przykład
Dla płaszczyzny \((100)\) mamy:
\( (100) \rightarrow \left(1, \,\ 0,\,\ -(1+0), \,\ 0 \right) \rightarrow (1 0 \bar 1 0) \)
Oznaczenie kierunków krystalograficznych
Opis kierunków krystalograficznych przy pomocy notacji Millera-Bravais'go jest nieco bardziej złożony. W celu zamiany wskaźników \([UVH]\) na notację Millera-Bravais'go \([uvtw] \) należy zastosować poniższe relacje:
\( u =\frac{1}{3} (2 U - V) \) , \( v =\frac{1}{3} (2 V - U) \) , \( t = - \frac{1}{3} (V + U) \) , w = W
Jeśli w wyniku obliczeń wartości \(u\), \(v\) oraz \(t\) uzyskamy wartości ułamkowe to należy pomnożyć wszystkie wskaźniki przez możliwie małą liczbę całkowitą.
Rysunek 2 przedstawia przykładowe kierunki wzdłuż wektorów prostych zapisane przy pomocy obu notacji.
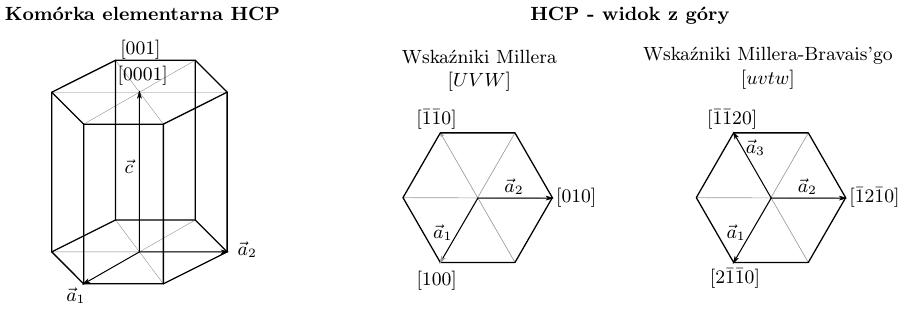 Rys. 2. Oznaczenie kierunków w notacji Millera oraz Millera-Bravais'go dla struktury HCP.
Rys. 2. Oznaczenie kierunków w notacji Millera oraz Millera-Bravais'go dla struktury HCP.
Przykład
Dla kierunku wzdłuż wektora \(\vec a_1\) oznaczonego przez wskaźniki Millera jako \([1 00]\) dokonujemy następujących przeliczeń:
\( [1 0 0] \rightarrow \left[ \left(\frac{1}{3}(2 - 0)\right) , \left(\frac{1}{3}(0 - 1)\right) , \left(- \frac{1}{3}(1 + 0)\right), 0 \right] \rightarrow \left[ \frac{2}{3}, -\frac{1}{3}, -\frac{1}{3}, 0 \right] \rightarrow [2 \bar 1 \bar 1 0] \)


